オーダー記法とは?簡単に説明
オーダー記法とは
「データ数が十分大きい時のアルゴリズムの計算量を大雑把に評価したものを記す方法」
のことです。
もっとざっくり簡単に言うと
「これを計算するのにどのくらいどれくらい時間がかかるのか?」
というのを表すものになります。
大雑把に評価するというものなので、細かい違いはあっても、大体同じくらいの計算時間だよねーというものは同じオーダーで表されることになります。
書き方
こんな感じで書きます⇩
O(n)
O(n²)
O(logn)
Oは「オーダー」の頭文字でアルファベットのオーです。
この場合だと、計算量は以下の順番で大きい(計算に時間がかかる)ことになります。
O(n²) > O(n) > O(logn)
計算量のざっくりとした見かたとしては
O(n)の場合はデータ量に比例して計算量が増えていく、
O(n²)の場合はデータ量に対して2次関数のように計算量が増えていく、
O(logn)の場合はデータ量に対してlog関数のように計算量が増えていく
ということになります。
logってなんぞ?という方は以下の記事を参照⇩
準備中・・・
では、実際にどのようにして計算量を算出していくのか。
その方法について具体例を使って見ていきましょう。
計算量算出の具体例
数当てゲームをしましょう。
私が1~16の数字を思い浮かべるので、
あなたはそれを言い当ててください。
YESまたはNOで答えられる質問をしてよいことにします。
何回の質問で数字を言い当てることができるでしょうか?
ここでは特に有名な
「線形探索」という方法と「2分探索」という方法を例にして正解を当てる方法を見ていきます。
線形探索
1つ目のやり方はこう。
1から順番にしらみつぶしで数字を聞いていきます。
1ですか?→NO
2ですか?→NO
3ですか?→NO
・・・
9ですか?→YES
⇒答えは9
といった具合です。
このように、順番にしらみつぶしに探し物をする方法を
「線形探索」と呼びます。
2分探索
2つ目のやり方はこう。
ある数字よりも大きいか小さいかを聞いていきます。
9以上ですか?→YES
13以上ですか?→NO
11以上ですか?→NO
10以上ですか?→NO
⇒答えは9
といった具合です。
このとき、数字は候補の中の真ん中の数字にすると、最も効率よく答えを絞っていくことができますよね。
真ん中の数字以上かどうかの質問を繰り返していくことで、
質問するごとに候補の数字を半分に絞っていくことができます。
このように候補を半分に絞っていきながら探し物をする方法を
「2分探索」と呼びます
より良いアルゴリズムはどちらか
この2つのアルゴリズムでは、どちらの方が効率的でしょうか?
※「アルゴリズム」は計算方法のことです
もちろん、2分探索の方が効率的なのは分かると思います。
実際に計算してみましょう。
データ数16の線形探索の計算時間
データ数16の線形探索の場合、
どれくらいの計算時間が必要かを求めてみましょう。
ここでは、「計算時間が大きい」=「質問の回数が多い」
ということにします。
まず、
数当てゲームの答えが「1」だった場合、
最初の質問で答えが分かるので最短の計算時間は「1」です。
数当てゲームの答えが「16」だった場合、
16回目の質問で答えが分かるので、最長の計算時間は「16」です。
このように2だった場合は計算時間が「2」、
3だった場合は計算時間が「3」
となるので、
計算時間の平均は以下のように計算できます。
(1+2+・・・+15+16) / 16 = 8.5
つまり、データ数16の線形探索は
最良計算時間が 1
最悪計算時間が 16
平均計算時間が 8.5
ということになります。
データ数16の2分探索の計算時間
データ数16の2分探索の場合は、
どれくらいの計算時間が必要になるか見てみましょう。
2分探索は、
最終的に1つに絞られるまで、候補が半分になる質問を繰り返していく方法でした。
なので、答えの数字が何であっても、
探索にかかる時間はかわりません。
1でも9でも16でも同じ回数の質問が必要になります。
データ数が16の場合は以下のように
データ数が絞られていきます。
16 → 8 → 4 → 2 → 1
つまり、データ数が16の2分探索は
最良計算時間が4
最悪計算時間が4
平均計算時間が4
ということになります。
データ数がnのときはどうなるか
では、データ数「16」ではなく、
より一般的にデータ数が「n」のときは計算時間はいくらになるでしょうか。
線形探索の場合
最良計算時間はたまたま1つ目で当たるかもしれないので「1」
最悪計算時間は最後まで当たらない場合なので「n」
平均計算時間はその平均なので「(1 + n) / 2」
になります。
2分探索の場合
2分探索の場合は線形探索より少し難しくなります。
データ数が16の場合の計算時間は「4」でした。
データ数が2倍になると質問の回数も1つ増えるので
データ数32の場合の計算時間は「5」になります。
データ数が半分になると、質問の回数が1つ減るので
データ数8の場合の計算時間は「3」になります。
これは以下のように書き換えることができます。
データ数が2³(= 8)の場合は計算時間が「3」
データ数が2⁴(= 16) の場合は計算時間が「4」
データ数が2⁵(= 32) の場合は計算時間が「5」
つまり、データ数が2の何乗になっているか?
の「何乗」の部分が、そのまま計算時間になるので、
2分探索の計算時間は「log₂n」になります。
オーダーはデータ数nのときの最悪計算時間
ここまで理解できた方は、
もうオーダー記法を理解するもう少しのところまできています。
オーダー記法は一般的に、ここまでで見てきた計算時間の
「データ数がnのときの最悪計算時間」
のこととほぼ同じ意味になります。
ですので、
線形探索アルゴリズムのオーダーはO(n)
2分探索アルゴリズムのオーダーはO(logn)
となります。
おやおや?logの底の「2」が消えてしまいました。
実は、実際の計算時間をオーダーに書き換えるときには、
以下のルールがあります。
★オーダーに書き換えるときのルール
1.最高次数以外の項は省く
2.係数は省く
3.対数の底は省く(常用対数とする)
算出した計算時間に対してこの3つのルールを当てはめていきます。
2分探索の場合は計算時間が「log₂n」だったので、
1.最高次数以外の項は省く
→項は1つなのでそのまま
2.係数は省く
→係数はないのでそのまま
3.対数の底は省く
→ log₂n ⇨ logn
となり、2分探索のオーダーは
O(logn)となります。
他にも例えば、計算時間を算出したら、
結果が『3n²+5n+100』
だったとします。
この時に上記ルールを適用すると
1.最高次数以外の項は省く
『 3n²+5n+100 』→『 3n²』
2.係数は省く
『 3n² 』→『 n² 』
対数は無いので、結果としてこのオーダーは
O(n²)となります。
別の例えでいくと
結果が『2nlog₂n + 100』
だっとすると
1.最高次数以外の項は省く
『2nlog₂n + 100』 →『 2nlog₂n 』
2.係数は省く
『 2nlog₂n 』→『 nlog₂n 』
3.対数の底は省く
『 nlog₂n 』→『 nlogn 』
結果としてこのオーダーは
O(nlogn)となります。
なぜ最高次数以外の項は省くのか
※理由に興味が無い人はここはスキップしてオッケーです
オーダー記法は「データ数が十分大きい時の計算量を大雑把に評価する方法」
でしたね。
・十分大きい
・大雑把
という2点が重要になってきます。
例えば計算時間が
① n³+n²+n
② n³
という2つの物があったとします。
データ数が10のときは
① 10³ + 10² + 10 = 1110
② 10³ = 1000
となって、差が11%くらいあります
データ数が10000のときはどうでしょう
① 10000³ + 10000² + 10000 = 1,000,100,010,000
② 10000³ = 1,000,000,000,000
となって、差が0.01%くらいになります。
データ数を∞にすると、この差は限りなく0に近づきますので、
オーダーを考えるときは
① n³+n²+n
② n³
この2つは同じことになりますので、
最高次数以外の項は省いてよい、ということになるのです。
なぜ係数は省いてよいのか
※理由に興味が無い人はここはスキップしてオッケーです
これは「データ数が増えるに従って、計算時間がどれだけ増えるのか」
を考えたときに、係数は関係ないことがわかります。
例えば計算時間が
① 3n
② n
という2つのものがあったとします
データ数が1のときは
① 3
② 1
になります。
データ数が10のときは
① 30
② 10
になります。
どちらも
「データ数が10倍になったら、計算量が10倍になる」
ことが分かると思います。
これは計算時間を大雑把に評価するときに同じ性能ということができるという考え方になります。
ですので、定数倍になるような係数は省いてよいと言うことになります。
なぜ対数の底は省いてよいのか
※理由に興味が無い人はここはスキップしてオッケーです
ここは1つ前に説明した
「なぜ係数は省いてよいのか」
という部分の考え方と全く同じになります。
対数の底の違いは、定数倍の違いでしかありません。
対数をグラフにすると以下のようになります。
※ここにグラフを入れる
それぞれ底の違うlog関数が定数倍の違いしかないため、
「なぜ係数は省いてよいのか?」の同じ理由で対数も省いてよいということになります。
まとめ
オーダー記法とは
「アルゴリズムの計算時間を大雑把に評価する方法」のこと
オーダー記法で計算量を求める方法
① データ数nでの最悪計算時間を求める
② 算出した最悪計算時間に、以下のルールを適用する
1.最高次数以外の項は省く
2.係数は省く
3.対数の底は省く(常用対数とする)
例題
以下のような数字が並んだ配列がある。
4 3 2 1
これを、昇順に並べ替えたい。
※昇順 = 左から小さい順
以下のルールに従って並べ替えを行う。
①一番左端を基準として、自分自身と1つ右を比較する
②比較した結果1つ右の方が小さい場合は自分自身と1つ右を入れ替える
③基準を1つ右に移動する
④上記操作を、1番右端との比較が完了するまで繰り返す
問題1
『4 3 2 1』に対して、上記①~④の操作を1回実施した結果を記してください。
問題2
『4 3 2 1』に対して上記①~④の操作をする際に比較した回数を答えてください。
問題3
『4 3 2 1』に対して上記①~④の操作をした配列に対して、
さらに①~④の操作を繰り返し実行し、昇順に並べ替え終わるまで繰り返してください。
問題4
『4 3 2 1』を昇順に並べ替えるまでに要した、合計の比較回数を答えてください。
問題5
数字の数がnこの配列に対して、同じように①~④の操作を繰り返し実行し、
並べ替えが完了するまでにかかる計算時間(比較回数)を算出してください。
例題6
このアルゴリズムのオーダーを答えてください。
例題の答え
問題1
答え:『 3 2 1 4 』
『4 3 2 1』を左端から順番に比較と交換を繰り返していくと以下のようになる。
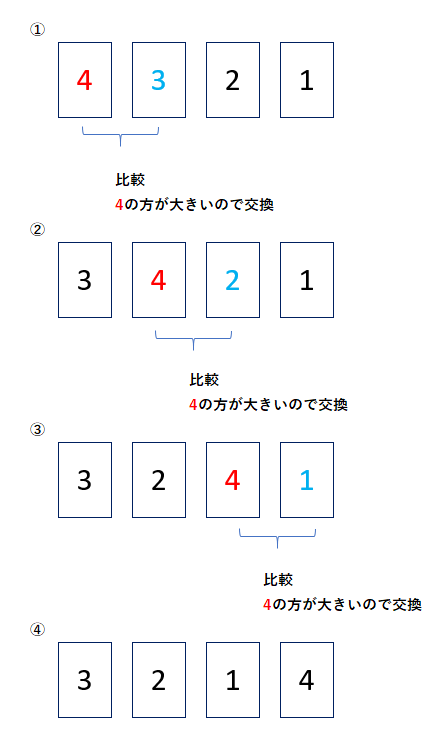
問題2
答え:3回
上記の図のように、データ数が4の配列に対して
①~④の操作を左端から右端まで行うと3回の操作が必要になる。
問題3
答え:『1 2 3 4』
以下の図のような流れになります。
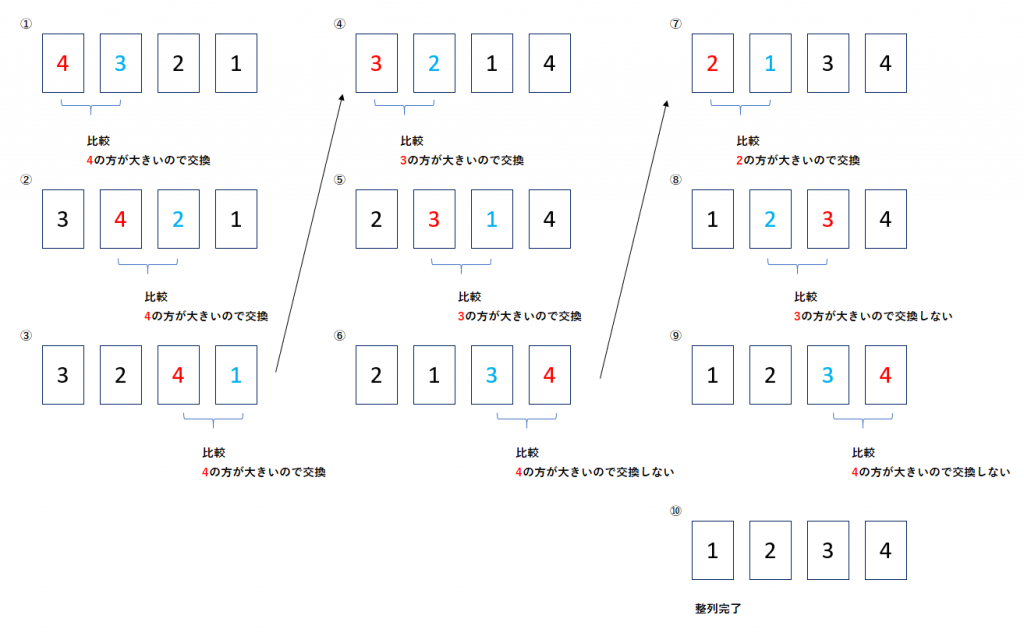
問題4
答え:9回
データ数4の配列の場合、
①~④の操作を右端まで行うのに必要な回数は3回でした。
この操作を1回行うと、
配列の中で一番大きい値が一番右端に来ることになります。
つまり、①~④の操作を右端まで繰り返しを1回行うと、4の整列が完了し、
もう一度①~④の操作を右端まで繰り返しを1回行うと、3の整列が完了し、
もう一度①~④の操作を右端まで繰り返しを1回行うと、2の整列が完了します。
2の整列まで完了したら、残りの1は自然と整列が完了しているので、これで全ての整列が完了したことになります。
①~④の操作に必要な回数が3回で、それを4,3,2それぞれの整列に対して行うので、3回×3回で9回の操作で並べ替えが完了することになります。
問題5
答え:(n – 1)²
データ数が4の場合は3×3の9回でした。
同様に、データ数がnの場合も、整列が必要な比較の回数は
(n – 1) × (n – 1) = (n – 1)²
となります。
問題6
答え:O(n²)
このアルゴリズムの計算時間は (n – 1)²
展開するとn² – 2n + 1となります。
これに対して、オーダーに書き換えるときの3つのルールを適用します。
1.最高次数以外は省く
n² – 2n + 1 → n²
2の係数はなく、3の対数も今回は登場しないので、結果として答えは
O(n²)
となります。
ちなみに
この整列アルゴリズムを『バブルソート』と呼びます。
データを昇順に並べ替えるときに、大きい値が右側に泡のように浮き上がって見えることからそう呼ばれているそうです。
例題の問題3を解いていて気付いた方もいるかもしれませんが、
このやり方には無駄があります。
①~④の操作を1回行うと、一番右端に一番大きい値が来るので、
次に①~④の操作を行うときは、一番右端は比較する必要がないのです。
つまり、データがnの場合、
1回目の①~④の操作は(n – 1)回必要ですが、
2回目の①~④の操作は、右端の比較の1回分をを省いて(n – 2)回で完了できます。
同様に、3回目は(n – 3)回、4回目は(n – 4)回と、比較する回数をだんだん少なくしていくことができます。
データ数が4の場合は以下のように、比較回数が6回で完了することになります。
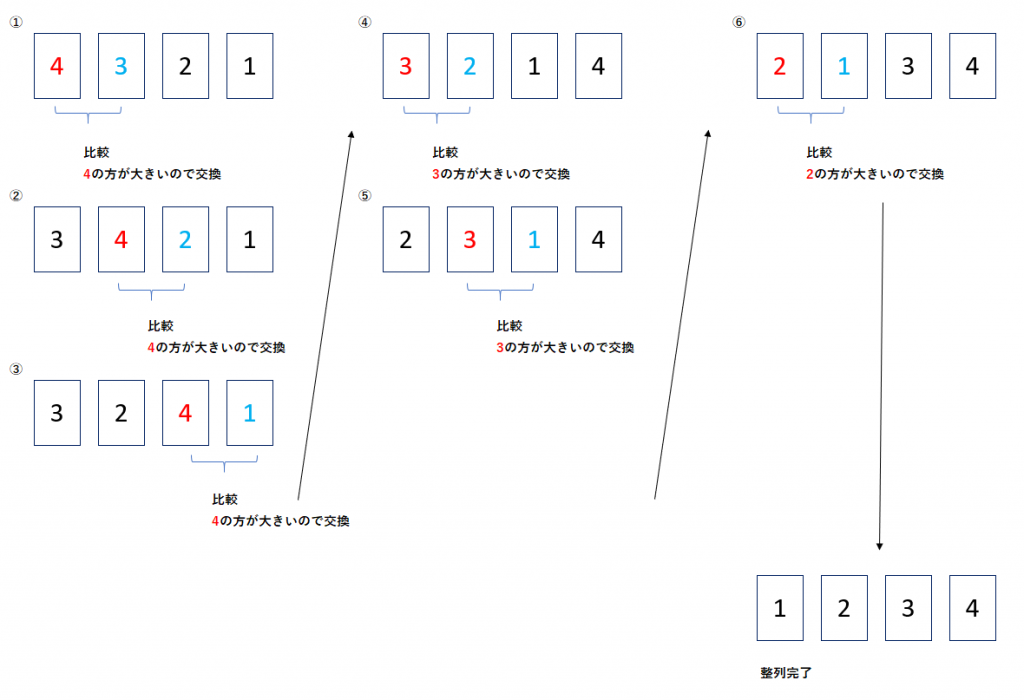
このアルゴリズムを『改良版バブルソート』と呼んだりしますが、
単にこちらのアルゴリズムをバブルソート呼んだりもします。
本質的な考え方は変わらないので、呼び方は重要ではないですが、
実際にコーディングする機会がもしあるなら、無駄を省いた改良版バブルソートにすることをオススメします。
改良版バブルソートの計算時間は以下のようになります。
(n – 1) + (n – 2) + ・・・ + 2 + 1 = n(n – 1)/ 2 = n²/2 – n/2
となり、オーダーは同じくO(n²)となります。
※初項1、公差1の等差数列の(n -1)までの和になります。ここでは解説は省きますので、ググってみてください。
練習問題
問題
以下のソートアルゴリズム(選択ソート)のオーダーを答えてください
①左端から右端までの値を走査し、最も小さい値を見つける
②見つけた最も小さい値と左端の値を入れ替える
③左から2番目の値から右端までの値を走査し、最も小さい値を見つける
④見つけた最も小さい値と左から2番目の値を入れ替える
⑤上記操作を、右端まで行う
ヒント
このアルゴリズムの計算時間は、①の最も小さい値を見つける操作に依存します。
1番目と2番目を比較して、小さい方を暫定の最小値とする、
3番目と暫定の最小値を比較して、小さい方を暫定の最小値とする・・・
この比較を右端まで繰り返したとき、最後に暫定の最小値となっていたものが最小値になります。
この比較回数がそのまま計算回数となります。
答え
O(n²)
解説
まず、①、②の操作を行います。
1.1番目と2番目を比較して、暫定の最小値を決定。
2.3番目と暫定の最小値を比較して、暫定の最小値を決定。
3.4番目と暫定の最小値を比較して、暫定の最小値を決定。
・・・・
n-1.n番目と暫定の最小値を比較して、最終的な最小値を決定。
ここまででn-1回の比較を行っていて、
最後に1番目の値と入れ替え操作を行います。
③、④の操作で次に2番目から右端までの最小値を決定して、2番目と最小値を入れ替えます。
この操作は、①、②に比べて1回少ない(1番目が整列完了しているため)ため、
比較回数はn-2回となります。
これを最後まで繰り返していくので、計算時間は
(n – 1) + (n – 2) + ・・・ + 2 + 1 = n(n – 1)/ 2 = n²/2 – n/2
となります。
結果として、オーダーはO(n²)となります。











最近のコメント